Terug naar de hoofdpagina
Terug naar het 'Random Archive'
Oud-examenvragen Burgies 1e kan KU Leuven '97-'98
(teksten in grijs zijn suggesties voor of verwijzingen naar oplossingen, de juistheid hiervan is niet gegarandeerd)
sqrt(x) staat voor "vierkantswortel van x" en ≤ ≥ betekenen respectievelijk "kleiner dan of gelijk aan" en "groter dan of gelijk aan" (een goede browser zou dit correct moeten weergeven, maar ja).
(Groep 1, Beirlant)
1. Geef de analogie tussen een diëlektrisch en een magnetisch materiaal (P,D/M,H)
2. Bereken de druk i.f.v. de gaskinetische grootheden. Wat is het verband met de ideale gaswet? (9.5)
3. Bereken σ (elektrische conductiviteit) i.f.v. het aantal vrije ladingsdragers n en i.f.v. τ (relaxatietijd) (7.11) en geef het verband met de wet van Ohm (7.12).
4. Geef het verband tussen warmteleer en diffusie (9.19, 7.13)
(Groep 2, Van Deynse)
1. Bespreek de wisselwerking tussen bewegende ladingen
2. a. 
Situeer in de cursus en bespreek de fysische betekenis (gedempte harmonische trilling, periodisch, aperiodisch, kritisch aperiodisch)
b. Bewijs dat 
(gewoon uitwerken)
c. Bespreek thermische uitzetting (a.d.h.v. inter-deeltjes interacties)
3. a. Bespreek de volgende uitspraak: de doorbuiging van een balk is een schuifvervorming (fout: longitudinale vervorming)
b. Geef een algemene methode voor het oplossen van elektrische ketens ("puzzelstukjes", zie les)
c. Hoe versterkt men de werking van een galvanometer of een elektrische motor? (door ijzeren kern in spoel te plaatsen wordt magnetische impedantie verminderd)
4. Bereken de druk i.f.v. de diepte in een vloeistof en pas toe op de berekening van de druk op een stuwdam en de druk i.f.v. hoogte in de atmosfeer.
1. Geef de definitie van dubbelpunt, leid de formules af en teken alle kwadrieken met een dubbelpunt.
2. V is de verzameling van alle 2×2 matrices A met A = ![[[a 0] [b c]]](burgimages/matrixa0bc.gif)
(a,b,c natuurlijke getallen)
Bewijs dat V een niet-commutatieve ring is voor de optelling en de vermenigvuldiging. (gewoon alle eigenschappen nagaan in formularium)
Bewijs dat 
een ring-homomorfisme is (idem) en pas de ontbindingsstelling toe.
3. Als P een n × n projectiematrix van rang r is, bespreek dan de eigenschappen van H = I - 2P. Wat is de rang van H?
Geef de eigenwaardenontbinding van H in termen van P. Illustreer met een niet-triviale 3 × 3 matrix van rang 2. Geef een geometrische interpretatie.
1. Theorievraag: Bespreek en bewijs de stelling die het bestaan garandeert van de singuliere waarden ontbinding. Hoe kan de SWO gebruikt worden voor het berekenen van de beste rang k benadering en voor de KKO van een stelsel. Geef ook een bewijs van de bewering. Illustreer voor de berekening van de SWO van A=[[1 2] [2 5]]
2. We noemen de orde m>0 van een permutatie het minimum aantal keer dat de permutatie met zichzelf moet samengesteld worden om de eenheid te verkrijgen. a) Construeer een permutatie van 1998 elementen die een orde 1997 heeft. Hoeveel mogelijkheden zijn er? (1998·1997!) b) Zijn er permutaties van 1998 elementen die een orde 2001 hebben? (ja) c) Zijn er permutaties van 1998 elementen die een orde 2003 hebben? (nee, 2003 is een priemgetal en kan dus niet ontbonden worden) Formuleer en bewijs hieruit een algemene eigenschap tussen het aantal elementen waarop een permutatie inwerkt en de orde van die permutatie.
3. Meetkundige plaats: Bepaal de vergelijking van de omwentelingsellipsoïde E met wentelas R: {x=0, y+z=0}. De ellipsoïde heeft ook twee raakvlakken V : x=-2 en W : 2x + (sqrt(2)+1)y + (sqrt(2)-1)z-8=0. Schets en bespreek ook de vorm van het oppervlak. (er is geen éénduidige oplossing).
1. Toon aan dat de eenbladige hyperboloide een regeloppervlak is. Geef en bewijs de eigenschappen van de stelsels rechten. Schets ook het oppervlak.
2. Construeer alle mogelijke permutaties π van de 11 elementen { a,b,c,d,e,f,g,h,i,j,k }, die aan de volgende twee eigenschappen voldoen 1) de afbeeldingen maken π(a)=b, π(b)=c, π(c)=d, π(e)=f, π(f)=g, en π(i)=h, 2) π15=I, met I de identieke permutatie π(x)=x voor alle x. Geef voor elke π de ontbinding in disjuncte cycli. (6 mogel.) 3) Vormen de machten van π nl πn voor n geheel een groep? (ja, zie formularium)
3. a) Verifieer dat het volgende stelsel AX=B strijdig is. b) Los het (indien mogelijk) op met de kleinste kwadratenmethode met de normaalvergelijkingen. (opl: X=[[2] [5]]) c) Los het op met de veralgemeende inverse via een singuliere waardenontbinding van A. d) Vergelijk de resultaten. (gelijk, natuurlijk) Kan het ook opgelost worden met een QR factorizatie van A? (ja, formule omvormen m.b.v. eigenschappen van Q en R)
A=[[1 0] [-1 1] [1 0] [-1 1]], B=[[1] [2] [3] [4]]
1. Geef de definitie van een spline-functie. Bespreek kubische splines. (bijvragen: is een spline een veeltermfunctie, hoeveel keer afleidbaar)
2. Onder welke voorwaarden geldt: 
? Bewijs. (zie stelling 4.4) Toon aan met een voorbeeld dat de voorwaarden voor de stelling nodig zijn. (voorbeeld 4.6)
3. Geef een gedetailleerd bewijs van het klein-criterium van Cauchy (LET OP: geef niet het 'bewijs' dat in de cursus staat, dat is allesbehalve 'gedetailleerd' en zal u gegarandeerd een 0 opleveren op deze vraag zelfs al is het letterlijk hetzelfde. Geef het bewijs dat Dierckx in de les gegeven heeft.)
4. Toon aan dat de arbeid nodig om een voorwerp langs een kromme C in een vectorveld te bewegen, gegeven wordt door de lijnintegraal over C. (uitrekenen zoals in de cursus)
1. Verklaar de volgende notaties:
f(x) = o(g(x)) ; x →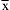 
f(x) = O(g(x)) ; x →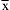
f(x) ~ g(x) ; x →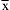
Zijn de volgende beweringen correct? Toon aan.
f(x) ~ g(x) ⇒ f(x) = O(g(x)) (juist)
f(x) ~ g(x) ⇒ f(x) = o(g(x)) (fout, ongelijke limieten (uitwerken))
2. Formuleer en bewijs de symmetrische vorm van de middelwaardestelling voor een functie van twee veranderlijken.
3. Behandel het probleem van de kleinste kwadratenrechte als een extremaalprobleem en werk uit. (ook aantonen dat oplossing minimum is, zoals in de cursus)
4. Formuleer en bewijs de stelling van Green. (volledig uitwerken)
April
1. Onderzoek de convergentie van de volgende oneigenlijke integralen:
Opmerking: log staat voor de natuurlijke logaritme.
2. (a) Bepaal yn(x) als oplossing van het beginwaardeprobleem
Controleer uw resultaat door in te vullen in de differentiaalvergelijking.
(b) Onderzoek de puntsgewijze convergentie van de rij {yn(x)}n≥1. Bepaal de limietfunctie en het convergentiedomein.
(c) Onderzoek de puntsgewijze convergentie van de rij {y'n(x)}n≥1. Bepaal de limietfunctie en het convergentiedomein.
(d) Onderzoek de gelijkmatige convergentie van {yn(x)}n≥1 en van {y'n(x)}n≥1 op het interval (
,0).
3. (a) Bereken de oppervlakte van het deel van de paraboloïde z = 4 - x2 - y2 dat gelegen is tussen de horizontale vlakken z = 0 en z = 3.
(b) Zij S het oppervlak van dezelfde paraboloïde, gelegen boven het x-y-vlak en links van het vlak x = 1(zie figuur), zo georiënteerd dat de normaalvector naar boven wijst. Bereken 
,
i. rechtstreeks als een oppervlakteintegraal
ii. als een lijnintegraal over de rand van het oppervlak
Opmerking: Geef duidelijk de door u gebruikte parametrisaties aan.
4. Beschouw de functie f(x,y) = (x2 - y2 - 9)(x2 - 25).
(a) Zoek de kritische punten van f(x,y) en bepaal de aard ervan.
(b) Maak een ruwe schets van de niveaulijnen f(x,y) = k op R = [-6,6] × [-6,6]. Maak een duidelijk onderscheid tussen de niveaulijnen voor k>0, k=0 en k<0. Duid de kritische punten aan op de figuur en het verloop van de niveaulijnen in hun omgeving.
(c) Zoek de punten waar f(x,y) haar globaal minimum en globaal maximum bereikt op de cirkel x2 + y2 = 25. Duid op de figuur de specifieke punten van de cirkel aan die je onderzocht hebt om tot het besluit te komen. Schets ook de niveaulijnen door deze punten.
Augustus
1. Onderzoek de convergentie van de volgende oneigenlijke integralen:
Opmerking: log staat voor de natuurlijke logaritme.
2. Beschouw de eerste-graadssplinefunctie:
fn(x) = (x + n + 1)1+ - 3 (x + n)1+ + 2 (x + n - 1)1+
(a) Schets de grafiek van de functies f1(x) en f2(x).
(b) Onderzoek de puntsgewijze en gelijkmatige convergentie van de rij {fn(x)}n≥1 op R.
(c) Onderzoek de puntsgewijze en gelijkmatige convergentie van de reeks
Zij s(x) de somfunctie van de reeks. Bereken s(0) en s(-2)
3. Bereken 
en C de kromme in het eerste kwadrant met als vergelijking in poolcoordinaten r = a sin(2θ),
(a) rechtstreeks (als een lijnintegraal),
(b) als een dubbele integraal over het gebied S omsloten door deze kromme.
4. Beschouw de functie f(x,y) = (y2-x2) (16x2 + 9y2 - 25).
(a) Maak een ruwe schets van de niveaulijnen f(x,y) = k op R = [-2,2] × [-2,2]. Maak een duidelijk onderscheid tussen de niveaulijnen voor k > 0, k = 0 en k < 0.
(b) Bereken de kritische punten van f(x,y) en bepaal de aard ervan. Duid de punten aan op uw figuur.
(c) Bereken de minimale en maximale waarde van f(x,y) op het cirkelvormig gebied D = {(x,y) | x2 + y2 ≤ 1}. Duid het gebied D aan op de figuur alsook de specifieke punten van D die je onderzocht hebt om tot het besluit te komen. Schets ook de niveaulijnen door en in de omgeving van deze punten.
1. Leid de verwachtingswaarde en de variantie af van het steekproefgemiddelde 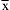(gewoon uitwerken)
en bereken de correlatie tussen het residu xi-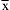 en 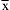(0, zie pag. 231). Welke veronderstellingen werden hiervoor gemaakt? (ze zijn bivariaat normaal verdeeld) Wat volgt hieruit voor 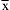en de variantie? (ze zijn onafhankelijk, zie pag. 230)
2. Er moeten n bytes verstuurd worden over een transmissielijn in paketten van K bytes. De kans op een slechte byte is 1/10000. Bepaal K zodat het aantal te versturen paketten minimaal is (zie les).
3. Oefening uit de oefenzittingen i.v.m. de opbrengst van 2 verschillende katalysatoren (is er met 5% sig.niveau een verschil in de opbrengst, bereken de nodige steekproefomvang om met 80% kans een verschil te detecteren enzovoort) (zie oefenzittingen)
4. Stel een kansverdeling op voor je score op dit examen, en geef een schatting voor de kans dat je geen 2e zit hebt. (nogal onduidelijke vraag maar volgens mij volstaat het om te zeggen dat de scores normaal verdeeld zijn en a.d.h.v. schattingen van de punten en varianties een schatting te maken van je score en de variantie ervan, die kan je dan gebruiken voor deel 2 van de vraag)
1. Stel de OC-curve op voor een hypothesetest van significantieniveau α voor het gemiddelde van een normaal verdeelde populatie met gekende variantie: H0: μ<=μ0 versus H1: μ>μ0 (zie cursus)
2. X1 en X2 zijn onafhankelijk en uniform verdeeld over [0,1]. Wat is de kansverdeling van Y=X1X2? ( FY(y)=y(1-ln(y)), fY(y)=-ln(y) )
3. Twee proffen nemen onafhankelijk elk 200 examens af. Het aantal geslaagde studenten is voor prof A 80 en voor prof B 96.
a. Is er bij een significantieniveau van 5% een significant verschil in de slaagkansen? (z0=-1.612, dus niet verwerpen, P-waarde=0.1074)
b. Men wenst met 90% kans een verschil van 5% tussen de slaagkansen te detecteren. Wat is het minimum aantal studenten dat elke prof moet ondervragen? (gebruik slaagkansen zodat dit minimum maximaal is).
4. Het nominale gewicht van een doos nagels is 50kg. Om ervoor te zorgen dat voldoende dozen dit gewicht halen, produceert men ze met een gemiddeld gewicht van 50.3kg en een variantie van 2.5kg2. Maak een aannemelijke veronderstelling voor de kansverdeling. (normaalverdeling wegens som van toevallige gewichten)
a. Voor welk percentage van de dozen ligt het gewicht boven het nominale gewicht? (57.5%)
b. Men houdt de variantie constant en wenst dat voor 97.5% van de dozen het gewicht boven het nominale niveau ligt. Welk gemiddelde moet men dan nastreven? (53.1kg)
c. Men houdt het gemiddelde constant, welke variantie moet men dan nastreven opdat het gewicht van 97.5% van de dozen boven het nominale niveau ligt? (σ2=0.0234 kg2)
1 en 2. 2 oefeningen (o.a. over chemisch evenwicht)
3. Bespreek de ontginning van Mg uit zeewater (zie auto-seminarie "Magnesium").
4. Geef het principe van Le Chatelier en pas toe op temperatuursverandering.
5. Geef de 3 massawetten en verklaar ze vanuit het atoommodel van Dalton.